Transcodages

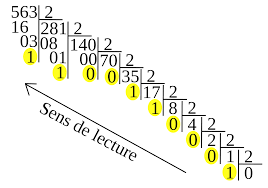
Les ordinateurs travaillent en binaire et les humains comptent en décimal. Il est indispensable de passer du code binaire au code décimal et réciproquement. Cela s'appelle le transcodage.

Du décimal vers le binaire : Sans utiliser de calculatrice, il existe au moins 2 méthodes pour transcoder du décimal en binaire : la division euclidienne et le tableau de conversion.

La division euclidienne : On divise successivement par 2 la valeur à convertir et on lit le reste (0 ou 1) du dernier vers le premier. Le résutat se lit de droite à gauche en remontant.

Dans l'exemple proposé à droite 563 est divisé par 2 une dizaine de fois. Il faut, à chaque fois, que le reste fasse 0 ou 1. Dès que le résultat de la division fait 0, on recopie de gauche à droite en remontant tous les restes pour lire le résutat de la conversion (du transcodage).

Ainsi pour 563(10), on lit 563 en base 10, on obtient 1000110011(2).

Remarque : un nombre 1011010 (par exemple) écrit dans une base (2 par exemple) se symbolise de la manière suivante : 1011010 ^² , donc 563(10)s'écrit aussi 563 ^¹⁰

Pour transcoder avec un tableau de conversion on construit un tableau ou apparaissent les puissances binaires et leurs valeurs en décimal. On place ensuite 1 dans la colonne binaire quand elle est contenue dans le nombre décimal et 0 sinon. (ne pas oublier de faire les soustractions) : le résutat se lit de gauche à droite :

Tableau de conversion :

Exemples : le tableau suivant permet d'établir la conversion entre décimal et binaire.

Conversion de 234 ^¹⁰ en binaire :

Méthode de remplissage :

Puissance binaire	2⁹	2⁸	2⁷	2⁶	2⁵	2⁴	2³	2²	2¹	2⁰
Valeur décimale	512	256	128	64	32	16	8	4	2	1
Résultat binaire	0	0	1	1	1	0	1	0	1	0

Dans le tableau on voit que 234 ne comprend pas 512 ni 256 mais comprends bien 128. On mets 0 dans la colonne quand ce n'est pas dans le nombre.

234 - 128 reste 106 ; on a bien une fois 64 et une fois 32 dans 106. On mets 1 quand c'est dans le nombre

106 - 64 reste 42 et 42 - 32 reste 10. 10 c'est 8 + 2, on mets donc 1 dans ces 2 colonnes et tout le reste à 0.

La conversion de 234 ^¹⁰ en binaire donne donc: 11101010 ^². (On n'écrit pas les premiers 0 qui ne sont pas significatifs)

En application : convertir en binaire par les 2 méthodes 543 ^¹⁰ et 1515 ^¹⁰

Du Binaire vers le décimal : On utilise les puissances de 2 ou le tableau.

Exemple : Convertissons 10101011 ^² en décimal. Cela fait 2⁰ + 2¹ + 2³ + 2⁵ + 2⁷ soit 1 + 2 + 8 + 32 + 128 = 171 ^¹⁰

Avec le tableau de conversion : Le principe est le même, on écrit le nombre binaire dans le tableau et on additionne les valeurs décimales quand on a 1 dans la colonne.

Exemple : Convertissons 1011101 ^² en décimal.

Puissance binaire	2⁹	2⁸	2⁷	2⁶	2⁵	2⁴	2³	2²	2¹	2⁰
Valeur décimale	512	256	128	64	32	16	8	4	2	1
Résultat binaire	0	0	0	1	0	1	1	1	0	1

Dans le tableau les cases qui ne servent pas sont à 0. On mets 1 dans la colonne quand la valeur décimale est dans le nombre.

64 + 16 + 8 + 4 + 1 = 93

La conversion de 1011101 ^² en binaire donne donc: 93 ^¹⁰.

En application : convertir en décimal 10110101 ^² et 1111000101 ^²